Q-обучение: от экспериментов Павлова до современной нейрореабилитации

Q-learning (Q-обучение на испанском) претерпел значительную эволюцию с первых поведенческих экспериментов, таких как классическое обусловливание Павлова, и стал одной из важнейших техник в области машинного обучения. Ниже мы рассмотрим, как развивалась эта технология и как она применяется в нейрореабилитации и когнитивной стимуляции.

Эксперименты Павлова

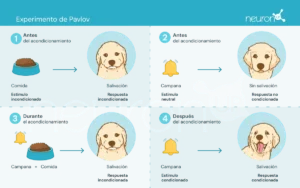
Иван Павлов, русский физиолог конца XIX века, известен тем, что заложил основы бихевиористской психологии через свои эксперименты по классическому обусловливанию. В этих экспериментах Павлов показал, что собаки могут научиться ассоциировать нейтральный стимул, например звук колокольчика, с безусловным стимулом, таким как еда, вызывая тем самым безусловную реакцию: слюноотделение.

Этот эксперимент был ключевым для демонстрации того, что поведение может быть приобретено посредством ассоциации — концепция, имевшая решающее влияние на развитие теорий обучения с подкреплением. 

Теории обучения с подкреплением

Эти теории сосредоточены на том, как люди и животные изучают поведение на основе последствий своих действий, что стало основой для разработки алгоритмов, таких как Q-learning.

Есть несколько ключевых понятий, с которыми стоит познакомиться перед продолжением:

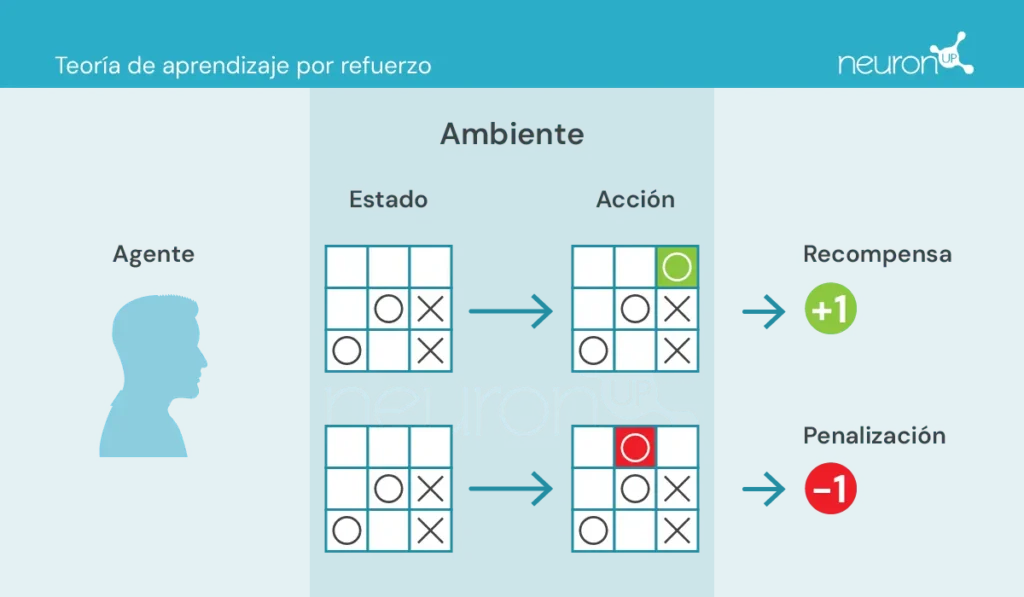
• Агент: тот, кто выполняет действие.
• Окружение: среда, в которой агент перемещается и взаимодействует. 
• Состояние: текущее положение дел в окружении. 
• Действие: возможные решения, принимаемые агентом.
• Награда: вознаграждения, присуждаемые агенту.

В этом типе обучения агент предпринимает действия в среде, получает информацию в виде награды/штрафа и использует её для корректировки своего поведения с течением времени.

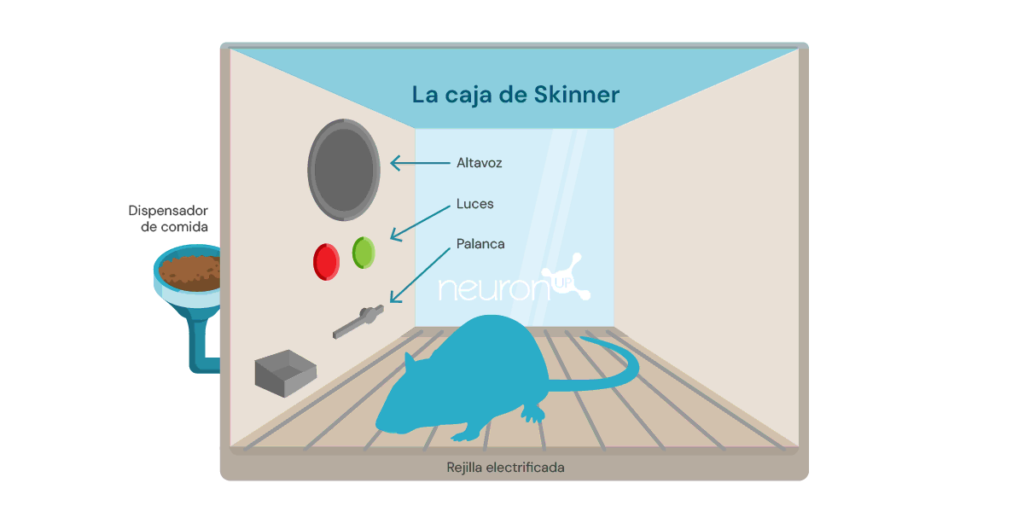
Классическим экспериментом в области обучения с подкреплением является эксперимент со ящиком Скиннера, проведённый американским психологом Беррхусом Фредериком Скиннером в 1938 году. В этом эксперименте Скиннер показал, что крысы могут научиться нажимать рычаг, чтобы получить еду, используя положительное подкрепление как средство формирования поведения. 

Эксперимент заключался в помещении крысы в коробку с рычагом, который она могла нажимать, с диспенсером для еды и иногда с лампой и динамиком. 

Каждый раз, когда крыса нажимала рычаг, в диспенсер выбрасывалась кормовая гранула. Еда действовала как положительное подкрепление — вознаграждение за нажатие рычага. Со временем крыса начинала нажимать рычаг чаще, демонстрируя, что она усвоила поведение через подкрепление.

Этот тип обучения послужил основой для алгоритмов машинного обучения, таких как Q-learning, который позволяет машинам самостоятельно вырабатывать оптимальное поведение методом проб и ошибок.

Что такое Q-learning?

Q-learning был представлен Кристофером Уоткинсом в 1989 году как алгоритм обучения с подкреплением. Этот алгоритм позволяет агенту узнать ценность действий в заданном состоянии, постоянно обновляя свои знания на основе опыта, подобно крысе в ящике Скиннера.

В отличие от экспериментов Павлова, где обучение основывалось на простых ассоциациях, Q-learning использует более сложный метод проб и ошибок. Агент исследует различные действия и обновляет Q-таблицу, в которой хранятся значения Q — ожидаемые будущие вознаграждения за выбор наилучшего действия в конкретном состоянии.

Q-learning применяется в различных областях, например в системах рекомендаций (как у Netflix или Spotify), в автономных транспортных средствах (дроны или роботы) и в оптимизации ресурсов. Далее мы рассмотрим, как эта технология может применяться в нейрореабилитации.

Q-learning и NeuronUP

Одно из преимуществ NeuronUP, — способность персонализировать упражнения в соответствии с конкретными потребностями каждого пользователя. Однако настройка каждой активности может быть утомительной из‑за большого числа параметров, требующих регулировки. 

Q-learning позволяет автоматизировать этот процесс, корректируя параметры в зависимости от результатов пользователя в различных заданиях. Это гарантирует, что упражнения будут сложными, но достижимыми, повышая эффективность и мотивацию в ходе реабилитации.

Как это работает?

В данном контексте агент, которого можно сравнить с пользователем, взаимодействующим с заданием, учится принимать оптимальные решения в разных ситуациях, чтобы успешно выполнить задачу. 

Q-learning позволяет агенту экспериментировать с разными действиями, взаимодействуя со своей средой, получать награды или наказания и обновлять Q-таблицу, в которой хранятся эти значения Q. Эти значения отражают ожидаемые будущие вознаграждения за выбор наилучшего действия в конкретном состоянии. 

Правило обновления Q-learning выглядит следующим образом:

\[Q(s,a) \leftarrow Q(s,a) + \alpha\bigl(r + \gamma \cdot \max_{a’}\bigl(Q(s’,a’)\bigr) — Q(s,a)\bigr)\]

Где:

𝛂 — это скорость обучения.

r — это награда, полученная после выполнения действия a из состояния s.

𝛄 — это коэффициент дисконтирования, который отражает важность будущих вознаграждений.

s’ — это следующее состояние.

\(\max_{a’}\bigl(Q(s’,a’)\bigr)\) — это максимальное значение Q для следующего состояния s’.

Пример применения в активности NeuronUP

Возьмём активность NeuronUP под названием «Imágenes revueltas», которая тренирует такие навыки, как планирование, визоконструктивные праксии и пространственные отношения. В этой задаче цель — собрать пазл, который был перемешан и разрезан на кусочки. 

Переменные, определяющие сложность этой активности, — это размер матрицы (число строк и столбцов) и степень перемешивания кусочков (низкая, средняя, высокая или очень высокая). 

Чтобы обучить агента собирать пазл, была создана матрица вознаграждений, основанная на минимальном числе ходов, необходимых для решения, определяемом следующей формулой:

\[\mathrm{Min\_Attempts} \;=\;\left\lceil \frac{\mathrm{factor} * \mathrm{rows} * \mathrm{columns}}{5}\right\rceil,\quad \mathrm{factor}\in\{1,3,5,7\}\]

Переменная factor зависит от уровня перемешивания. После построения матрицы был применён алгоритм Q-learning для обучения агента автоматическому решению пазла. 

Эта интеграция включает:

• Получение значения Q: Функция извлекает значение Q для пары состояние-действие из Q-таблицы. Если пара состояние-действие ранее не была обучена, возвращается 0. Эта функция ищет ожидаемую награду за выполнение конкретного действия в конкретном состоянии.
• Обновление значения Q: Функция обновляет значение Q для пары состояние-действие на основе полученной награды и максимального значения Q следующего состояния. Эта функция реализует правило обновления Q-learning, описанное выше.
• Решение о действии: Функция решает, какое действие выполнить в данном состоянии, используя стратегию epsilon-greedy. Эта стратегия балансирует между исследованием и эксплуатацией: 
  • Исследование: Заключается в выборе известных наилучших действий до настоящего момента. С вероятностью ε (коэффициент исследования, значение между 0 и 1, определяющее вероятность изучения новых действий вместо использования известных) выбирается случайное действие, что позволяет агенту обнаруживать потенциально лучшие действия. 
  •  Эксплуатация: Заключается в проверке действий, отличных от известных лучших, чтобы выяснить, могут ли они обеспечить лучшие награды в будущем. С вероятностью 1−ε агент выбирает действие с наивысшим значением Q для текущего состояния, используя накопленные знания: a’ = argmaxaQ(s,a). Где a’ — действие, максимизирующее функцию Q в состоянии s. Это означает, что для данного состояния s выбирается действие a с наибольшим значением Q.

Эти функции работают совместно, чтобы позволить алгоритму Q-learning разработать оптимальную стратегию для решения пазла.

Предварительный анализ выполнения алгоритма

Алгоритм был применён к пазлу размером матрицы 2×3 с коэффициентом сложности 1 (низкий), соответствующим минимальному числу попыток, равному 2. Алгоритм запускали на одном и том же пазле 20 раз, применяя одинаковую настройку перемешивания при каждом запуске и обновляя Q-таблицу после каждого шага. После 20 запусков пазл перемешивали в другой конфигурации и процесс повторялся, в результате чего было получено в общей сложности 2000 итераций. Начальные значения параметров были: 

• Награда за решение пазла: 100 очков 
• Штраф за каждый ход: -1 очко

На каждом шаге применялась дополнительная награда или штраф, основанные на количестве правильно расположенных кусочков, что позволяло агенту понимать прогресс в достижении решения пазла. Это рассчитывалось по формуле:

\[W \times \bigl(N_{\mathrm{correct}}^i \;-\; N_{\mathrm{correct}}^{\,i-1}\bigr)\]

Где:

• W — коэффициент веса.
• \(N_{\mathrm{correct}}^{\,i}\) — число правильных кусочков после хода.
• \(N_{\mathrm{correct}}^{\,i-1}\) — число правильных кусочков до хода.

График ниже иллюстрирует число ходов, требуемых по итерациям, чтобы модель решила пазл размера 2×3. В начале модель требует большого числа ходов, что отражает отсутствие знаний о том, как эффективно решать пазл. Однако по мере обучения алгоритма Q-learning наблюдается нисходящая тенденция в числе ходов, что свидетельствует о том, что модель учится оптимизировать процесс решения.

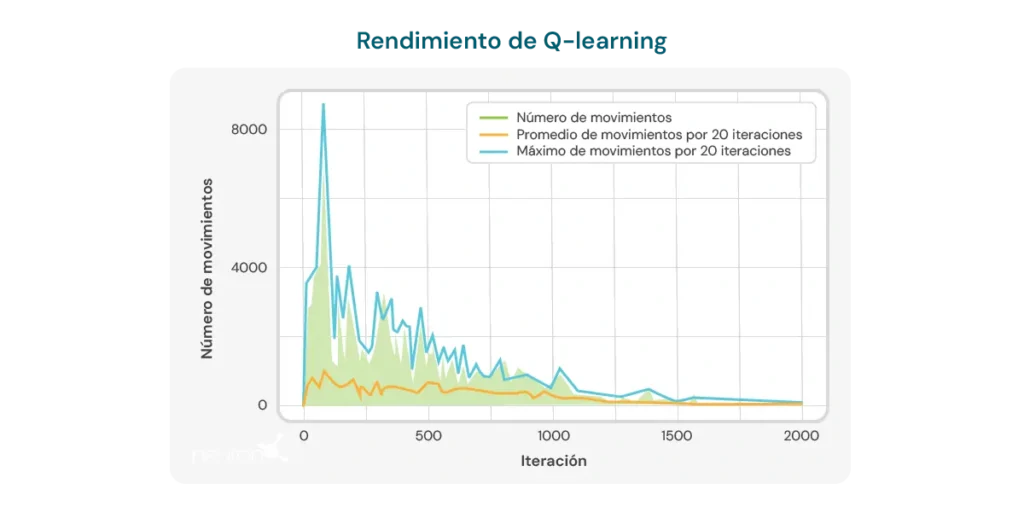
Эта тенденция является положительным признаком потенциала алгоритма для улучшения с течением времени. Тем не менее, следует учитывать несколько важных ограничений:

• Специфический размер пазла: Алгоритм демонстрирует эффективность в основном для пазлов определённого размера, например матрицы 2×3. При изменении размера или сложности пазла производительность алгоритма может значительно снизиться.
• Время вычислений: При применении алгоритма к другим или более сложным конфигурациям время, необходимое для вычислений и решения пазла, значительно увеличивается. Это ограничивает его применение в ситуациях, требующих быстрой реакции, или в более сложных пазлах.
• Число ходов всё ещё велико: Несмотря на наблюдаемое улучшение, число ходов, требуемых для решения пазла, остаётся относительно высоким даже после множества итераций. В последних запусках модель требует в среднем 8–10 ходов, что указывает на потенциал для повышения эффективности обучения.

Эти ограничения подчёркивают необходимость дальнейшей доработки алгоритма — будь то настройка параметров обучения, улучшение структуры модели или включение дополнительных методов, позволяющих добиться более эффективного и адаптивного обучения для разных конфигураций пазлов. Несмотря на эти ограничения, не стоит забывать о преимуществах Q-learning в нейрореабилитации, среди которых:

• Динамическая персонализация активностей: Q-learning способен автоматически корректировать параметры терапевтических занятий в зависимости от индивидуальных результатов пользователя. Это означает, что активности могут персонализироваться в реальном времени, обеспечивая такой уровень сложности, который является одновременно требовательным и достижимым. Это особенно полезно в нейрореабилитации, где способности пользователей могут существенно отличаться и изменяться со временем.
• Повышение мотивации и вовлечённости: По мере того как активности постоянно адаптируются под уровень навыков пользователя, уменьшаются фрустрация от слишком сложных задач и скука от слишком простых. Это может значительно повысить мотивацию пользователя и его вовлечённость в программу реабилитации, что критично для достижения успешных результатов.
• Оптимизация процесса обучения: Используя Q-learning, система может учиться на предыдущих взаимодействиях пользователя с активностями, оптимизируя процесс обучения и реабилитации. Это позволяет делать упражнения более эффективными, сосредотачиваясь на зонах, где пользователь нуждается в дополнительной работе, и сокращая время, необходимое для достижения терапевтических целей.
• Эффективность при принятии клинических решений: Специалисты могут извлечь пользу из Q-learning, получая рекомендации на основе данных о том, как корректировать терапии. Это облегчает принятие более обоснованных и точных клинических решений, что, в свою очередь, повышает качество предоставляемой помощи пользователю.
• Постоянное улучшение: Со временем система на основе Q-learning может повышать свою эффективность благодаря накоплению данных и опыту пользователей. Это означает, что чем больше используется система, тем эффективнее она становится в персонализации и оптимизации упражнений, предоставляя долгосрочное преимущество в процессе нейрореабилитации.

В заключение, Q-learning прошёл путь от корней в бихевиористской психологии до мощного инструмента в искусственном интеллекте и нейрореабилитации. Его способность самостоятельно адаптировать активности делает его ценным ресурсом для повышения эффективности терапий восстановления, хотя остаются задачи, которые необходимо решить для полной оптимизации его применения.

Библиография

• Bermejo Fernández, E. (2017). Применение алгоритмов обучения с подкреплением к играм.
• Giró Gràcia, X., & Sancho Gil, J. M. (2022). Искусственный интеллект в образовании: большие данные, чёрные ящики и технологический солюционизм.
• Meyn, S. (2023). Stability of Q-learning through design and optimism. arXiv preprint arXiv:2307.02632.
• Morinigo, C., & Fenner, I. (2021). Теории обучения. Minerva Magazine of Science, 9(2), 1-36.
• M.-V. Aponte, G. Levieux y S. Natkin. (2009). Measuring the level of difficulty in single player video games. Entertainment Computing.
• P. Jan L., H. Bruce D., P. Shashank, B. Corinne J., & M. Andrew P. (2019). The Effect of Adaptive Difficulty Adjustment on the Effectiveness of a Game to Develop Executive Function Skills for Learners of Different Ages. Cognitive Development, pp. 49, 56–67.
• R. Anna N., Z. Matei & G. Thomas L. Optimally Designing Games for Cognitive Science Research. Computer Science Division and Department of Psychology, University of California, Berkeley.
• Toledo Sánchez, M. (2024). Применение обучения с подкреплением в видеоиграх.

Если вам понравилась эта статья о Q-learning, вас наверняка заинтересуют следующие материалы NeuronUP:

«Эта статья была переведена. Ссылка на оригинальную статью на испанском:»
Q-learning: Desde los experimentos de Pavlov a la neurorrehabilitación moderna