Il Q-learning (apprendimento Q in italiano) è evoluto notevolmente dagli esperimenti comportamentali iniziali, come il condizionamento classico di Pavlov, fino a diventare una delle tecniche più importanti nell’ambito del Machine Learning (apprendimento automatico). Di seguito esploreremo come si è sviluppato e la sua applicazione nella neuroriabilitazione e nella stimolazione cognitiva.
Gli esperimenti di Pavlov
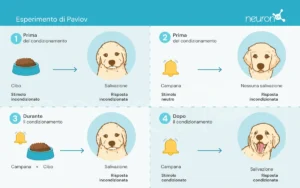
Ivan Pavlov, un fisiologo russo della fine del XIX secolo, è riconosciuto per aver stabilito le basi della psicologia comportamentale attraverso i suoi esperimenti sul condizionamento classico. In questi esperimenti, Pavlov dimostrò che i cani potevano imparare ad associare uno stimolo neutro, come il suono di una campana, con uno stimolo incondizionato, come il cibo, provocando così una risposta incondizionata: la salivazione.
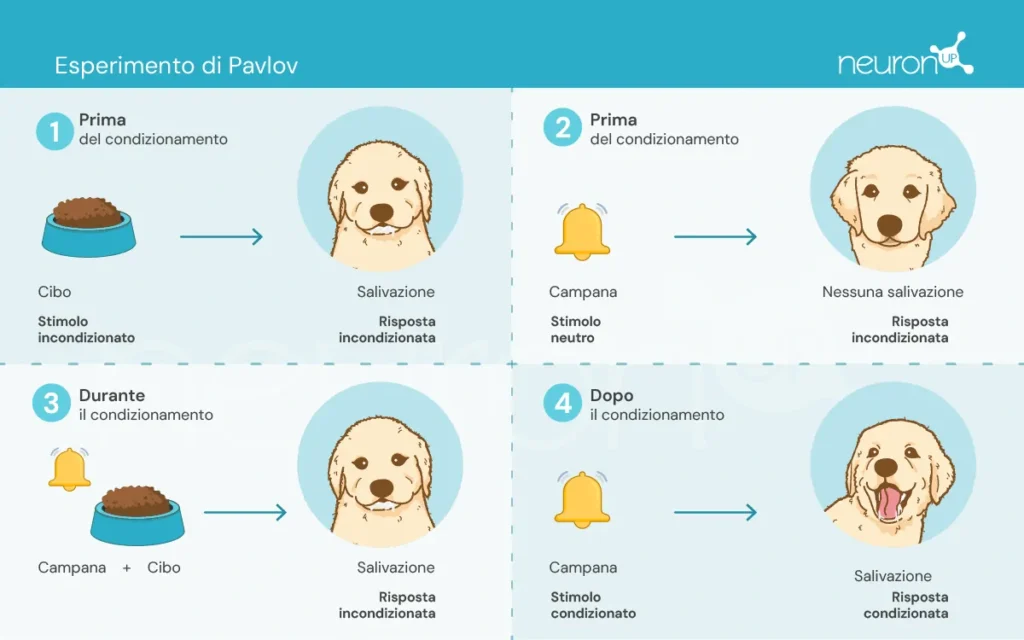
Questo esperimento fu fondamentale per dimostrare che il comportamento può essere acquisito per associazione, un concetto cruciale che successivamente ha influenzato lo sviluppo delle teorie di apprendimento per rinforzo.
Le teorie dell’apprendimento per rinforzo
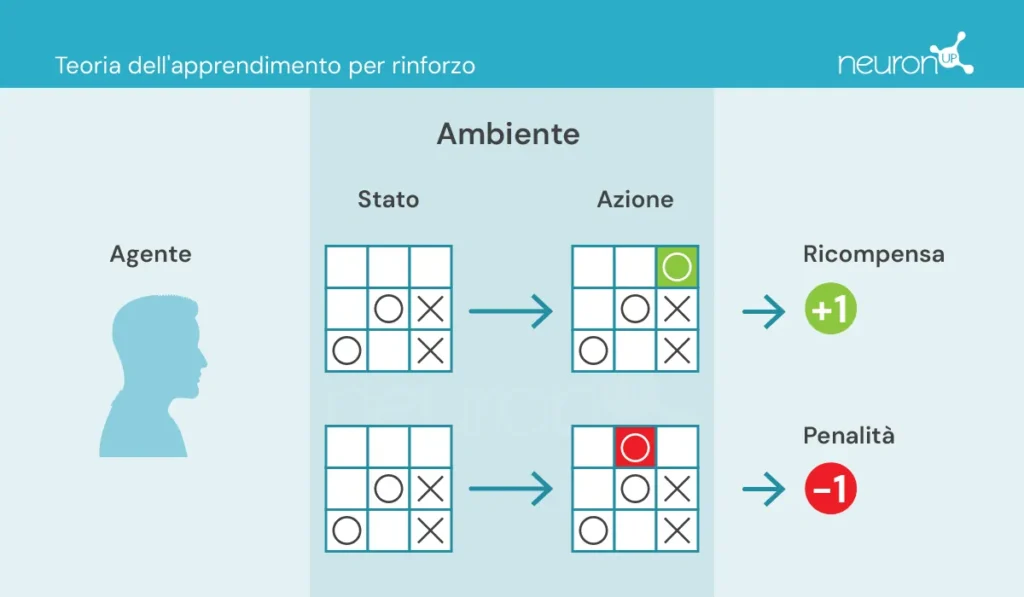
Queste teorie si concentrano su come gli esseri umani e gli animali apprendano comportamenti a partire dalle conseguenze delle loro azioni, un principio fondamentale per il design di algoritmi come il Q-learning.
Ci sono alcuni concetti chiave con cui dobbiamo familiarizzare prima di continuare:
- Agente: responsabile dell’azione.
- Ambiente: contesto in cui l’agente si muove e interagisce.
- Stato: situazione attuale dell’ambiente.
- Azione: decisioni possibili prese dall’agente.
- Ricompensa: premi concessi all’agente.
In questo tipo di apprendimento, un agente compie o esegue azioni nell’ambiente, riceve informazioni sotto forma di ricompensa/penalizzazione e le utilizza per regolare il suo comportamento nel tempo.
Un classico esperimento di apprendimento per rinforzo è l’esperimento della scatola di Skinner, condotto dallo psicologo statunitense Burrhus Frederic Skinner nel 1938. In questo esperimento, Skinner dimostrò che i ratti potevano imparare a premere una leva per ottenere cibo, utilizzando il rinforzo positivo come mezzo per modellare il comportamento.
L’esperimento consiste nell’introdurre un ratto in una scatola con una leva che può premere, un distributore di cibo, e talvolta, una luce e un altoparlante.
Ogni volta che il ratto preme la leva, un chicco di cibo viene rilasciato nel distributore. Il cibo funge da rinforzo positivo, una ricompensa per aver premuto la leva. Col tempo, il ratto inizierà a premere la leva con maggiore frequenza, dimostrando di aver appreso il comportamento attraverso il rinforzo.
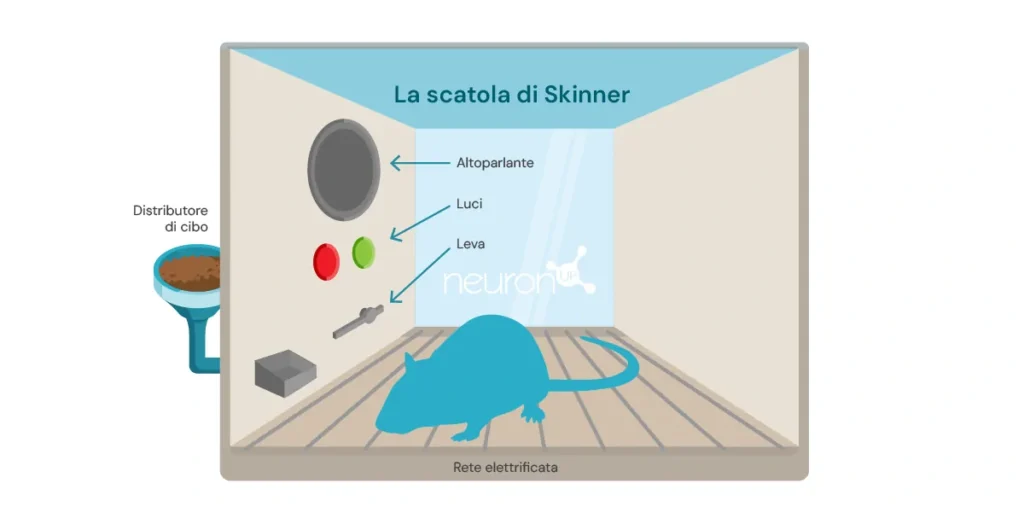
Questo tipo di apprendimento è servito come base per algoritmi di machine learning, come il Q-learning, che permette alle macchine di apprendere comportamenti ottimali in modo autonomo attraverso il metodo di tentativi ed errori.
Cos’è il Q-learning?
Il Q-learning fu introdotto da Christopher Watkins nel 1989 come un algoritmo di apprendimento per rinforzo. Questo algoritmo permette a un agente di apprendere il valore delle azioni in uno stato determinato, aggiornando continuamente le sue conoscenze attraverso l’esperienza, proprio come il ratto nella scatola di Skinner.
A differenza degli esperimenti di Pavlov, in cui l’apprendimento si basava su semplici associazioni, il Q-learning utilizza un metodo più complesso di tentativi ed errori. L’agente esplora diverse azioni e aggiorna una tabella Q che memorizza i valori Q, che rappresentano le ricompense future attese per intraprendere la migliore azione in uno stato specifico.
Il Q-learning si applica in diversi ambiti, ad esempio nei sistemi di raccomandazione (come quelli utilizzati da Netflix o Spotify), nei veicoli autonomi (come droni o robot) e nell’ottimizzazione delle risorse. Ora esploreremo come questa tecnologia può essere applicata nella neuroriabilitazione.
Q-learning e NeuronUP
Uno dei vantaggi di NeuronUP è la capacità di personalizzare le attività in base alle esigenze specifiche di ciascun utente. Tuttavia, personalizzare ogni attività può essere tedioso a causa dell’elevato numero di parametri da regolare.
Il Q-learning consente di automatizzare questo processo, regolando i parametri in funzione delle prestazioni dell’utente nelle diverse attività. Ciò garantisce che gli esercizi siano impegnativi ma raggiungibili, migliorando l’efficacia e la motivazione durante la riabilitazione.
Come funziona?
In questo contesto, l’agente, che potrebbe essere paragonato a un utente che interagisce con un’attività, impara a prendere decisioni ottimali in diverse situazioni per superare correttamente l’attività.
Il Q-learning consente all’agente di sperimentare con diverse azioni interagendo con il suo ambiente, ricevendo ricompense o penalizzazioni, e aggiornando una tabella Q che memorizza questi valori Q. Questi valori rappresentano le ricompense future attese per intraprendere la migliore azione in uno stato specifico.
La regola di aggiornamento del Q-learning è la seguente:
Dove:
𝛂 – è il tasso di apprendimento.
r – è la ricompensa ricevuta dopo aver eseguito l’azione a dallo stato s.
𝛄 – è il fattore di sconto, che rappresenta l’importanza delle ricompense future.
s’ – è il prossimo stato.
– è il valore Q massimo per il prossimo stato s’.

Iscriviti
alla nostra
Newsletter
Esempio di applicazione in un’attività di NeuronUP
Prendiamo l’attività di NeuronUP chiamata “Immagini confuse”, che allena abilità come la pianificazione, le prassie visuo-costruttive e la relazione spaziale. In questa attività, l’obiettivo è risolvere un puzzle che è stato mescolato e tagliato in pezzi. Questa attività non è ancora disponibile in italiano, ma è possibile trovarla in inglese, francese, spagnolo, portoghese e catalano.
Le variabili che definiscono la difficoltà di questa attività sono la dimensione della matrice (il numero di righe e colonne) e il valore del disordine dei pezzi (basso, medio, alto o molto alto).
Per addestrare l’agente a risolvere il puzzle, è stata creata una matrice di ricompense basata sul numero minimo di mosse necessarie per risolverlo, definito dalla seguente formula:
La variabile del fattore dipende dal livello di disordine. Una volta creata la matrice, è stato applicato un algoritmo di Q-learning per addestrare l’agente a risolvere il puzzle automaticamente.
Questa integrazione include:
- Recupero del valore Q: La funzione recupera il valore Q per una coppia stato-azione dalla tabella Q. Se la coppia stato-azione non è mai stata addestrata prima, restituisce 0. Questa funzione cerca la ricompensa prevista eseguendo un’azione specifica in uno stato specifico.
- Aggiornamento del valore Q: La funzione aggiorna il valore Q per una coppia stato-azione basata sulla ricompensa ricevuta e sul valore Q massimo dello stato successivo. Questa funzione implementa la regola di aggiornamento del Q-learning menzionata in precedenza.
- Decisione sull’azione da intraprendere: La funzione decide quale azione intraprendere in uno stato dato, utilizzando una strategia epsilon-greedy. Questa strategia bilancia esplorazione e sfruttamento:
- Esplorazione: Consiste nella selezione della migliore azione conosciuta fino a quel momento. Con una probabilità ε (tasso di esplorazione, un valore tra 0 e 1 che determina la probabilità di esplorare nuove azioni invece di sfruttare quelle conosciute), si sceglie un’azione casuale, consentendo all’agente di scoprire azioni potenzialmente migliori.
- Sfruttamento: Consiste nel testare azioni diverse dalle migliori conosciute per vedere se possono offrire migliori ricompense in futuro. Con una probabilità di 1−ε, l’agente seleziona l’azione con il valore Q più alto per lo stato attuale, utilizzando le sue conoscenze apprese: a’ = argmaxaQ(s,a). Dove a’ è l’azione che massimizza la funzione Q in uno stato s dato. Questo significa che, dato uno stato s, si seleziona l’azione a con il valore Q più alto.
Queste funzioni lavorano insieme per consentire all’algoritmo di Q-learning di sviluppare una strategia ottimale per risolvere il puzzle.
Analisi preliminare dell’esecuzione dell’algoritmo
L’algoritmo è stato applicato a un puzzle di matrice 2×3 con un fattore di difficoltà 1 (basso), corrispondente a un numero minimo di tentativi pari a 2. L’algoritmo è stato eseguito 20 volte sullo stesso puzzle, applicando la stessa configurazione di miscelazione ogni volta e aggiornando la tabella Q dopo ogni passaggio. Dopo 20 esecuzioni, il puzzle è stato miscelato in una configurazione diversa e il processo è stato ripetuto, risultando in un totale di 2000 iterazioni. I valori iniziali dei parametri erano:
- Ricompensa per la risoluzione del puzzle: 100 punti
- Penalità per ogni mossa: -1 punto
Ad ogni passo, veniva applicata una ricompensa o una penalità aggiuntiva basata sul numero di pezzi corretti, permettendo all’agente di comprendere il suo progresso verso la risoluzione del puzzle. Questo veniva calcolato utilizzando la formula:
Dove:
- W è il fattore di peso.
è il numero di pezzi corretti dopo il movimento.
è il numero di pezzi corretti prima del movimento.
Il grafico qui sotto illustra il numero di mosse necessarie per iterazione affinché il modello risolva un puzzle di dimensioni 2×3. All’inizio, il modello richiede un gran numero di mosse, riflettendo la sua mancanza di conoscenza su come risolvere il puzzle in modo efficiente. Tuttavia, man mano che l’algoritmo di Q-learning si allena, si osserva una tendenza al ribasso nel numero di mosse, suggerendo che il modello sta imparando a ottimizzare il suo processo di risoluzione.
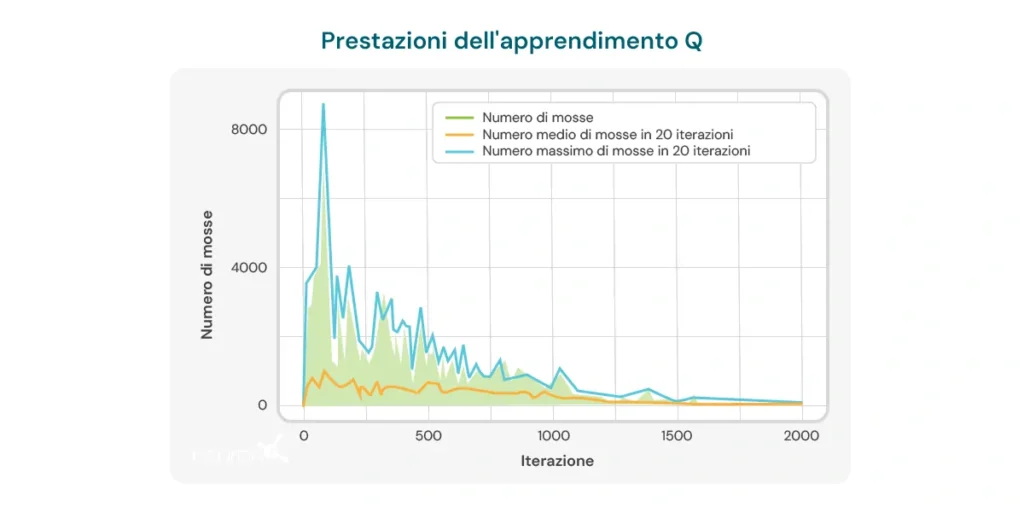
Questa tendenza è un segnale positivo del potenziale dell’algoritmo per migliorare nel tempo. Tuttavia, devono essere considerate diverse limitazioni importanti:
- Dimensione specifica del puzzle: L’algoritmo dimostra efficacia principalmente in puzzle con una dimensione specifica, come la matrice 2×3. Cambiando la dimensione o la complessità del puzzle, le prestazioni dell’algoritmo possono diminuire significativamente.
- Tempo di calcolo: Quando l’algoritmo viene applicato a configurazioni diverse o più complesse, il tempo necessario per eseguire i calcoli e risolvere il puzzle aumenta notevolmente. Questo ne limita l’applicabilità in situazioni che richiedono risposte rapide o in puzzle con maggiore complessità.
- Numero di mosse ancora elevato: Nonostante i miglioramenti osservati, il numero di mosse necessarie per risolvere il puzzle rimane relativamente elevato, anche dopo molteplici iterazioni. Nelle ultime esecuzioni, il modello richiede in media 8-10 mosse, il che indica che c’è ancora margine per migliorare l’efficienza dell’apprendimento.
Queste limitazioni evidenziano la necessità di un ulteriore affinamento dell’algoritmo, sia regolando i parametri di apprendimento, migliorando la struttura del modello o incorporando tecniche complementari che permettano un apprendimento più efficiente e adattabile a diverse configurazioni di puzzle. Nonostante queste limitazioni, non dobbiamo dimenticare i vantaggi che il Q-learning offre nella neuroriabilitazione, tra cui:
- La personalizzazione dinamica delle attività: Il Q-learning è in grado di regolare automaticamente i parametri delle attività terapeutiche in base alle prestazioni individuali dell’utente. Ciò significa che le attività possono essere personalizzate in tempo reale, assicurando che ogni utente lavori a un livello che sia stimolante ma raggiungibile. Questo è particolarmente utile nella neuroriabilitazione, dove le capacità degli utenti possono variare notevolmente e cambiare nel tempo.
- Aumento della motivazione e dell’impegno: Poiché le attività si adattano costantemente al livello di abilità dell’utente, si evita la frustrazione per compiti troppo difficili o la noia per compiti troppo semplici. Questo può aumentare significativamente la motivazione dell’utente e il suo impegno nel programma di riabilitazione, cruciale per ottenere risultati di successo.
- Ottimizzazione del processo di apprendimento: Utilizzando il Q-learning, il sistema può imparare dalle interazioni precedenti dell’utente con le attività, ottimizzando il processo di apprendimento e riabilitazione. Questo consente che gli esercizi siano più efficaci, concentrandosi sulle aree in cui l’utente ha bisogno di maggiore attenzione e riducendo il tempo necessario per raggiungere gli obiettivi terapeutici.
- Efficienza nel prendere decisioni cliniche: I professionisti possono beneficiare del Q-learning ottenendo raccomandazioni basate sui dati su come adattare le terapie. Questo facilita decisioni cliniche più informate e precise, migliorando così la qualità dell’assistenza fornita all’utente.
- Miglioramento continuo: Nel tempo, il sistema basato sul Q-learning può migliorare le sue prestazioni attraverso l’accumulo di dati e l’esperienza dell’utente. Questo significa che, più viene utilizzato il sistema, più efficace diventa nella personalizzazione e nell’ottimizzazione degli esercizi, offrendo così un vantaggio a lungo termine nel processo di neuroriabilitazione.
Concludendo, il Q-learning è evoluto dalle sue radici nella psicologia comportamentale fino a diventare uno strumento potente nell’intelligenza artificiale e nella neuroriabilitazione. La sua capacità di adattare autonomamente le attività lo rende una risorsa preziosa per migliorare l’efficacia delle terapie riabilitative, anche se rimangono sfide da superare per ottimizzare completamente la sua applicazione.
Bibliografia
- Bermejo Fernández, E. (2017). Applicazione di algoritmi di reinforcement learning ai giochi.
- Giró Gràcia, X., & Sancho Gil, J. M. (2022). L’Intelligenza Artificiale nell’educazione: Big data, scatole nere e soluzione tecnologica.
- Meyn, S. (2023). Stability of Q-learning through design and optimism. arXiv preprint arXiv:2307.02632.
- Morinigo, C., & Fenner, I. (2021). Teorie dell’apprendimento. Minerva Magazine of Science, 9(2), 1-36.
- M.-V. Aponte, G. Levieux e S. Natkin. (2009). Misurare il livello di difficoltà nei videogiochi per giocatori singoli. Entertainment Computing.
- P. Jan L., H. Bruce D., P. Shashank, B. Corinne J., & M. Andrew P. (2019). L’effetto dell’aggiustamento dinamico della difficoltà sull’efficacia di un gioco per sviluppare le abilità esecutive in studenti di diverse età. Cognitive Development, pp. 49, 56–67.
- R. Anna N., Z. Matei & G. Thomas L. Progettazione ottimale di giochi per la ricerca in scienze cognitive. Computer Science Division and Department of Psychology, University of California, Berkeley.
- Toledo Sánchez, M. (2024). Applicazioni del reinforcement learning nei videogiochi.
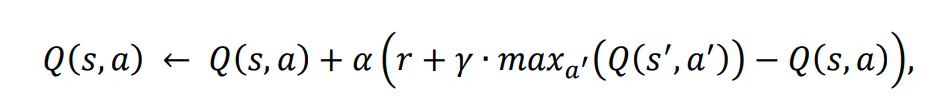
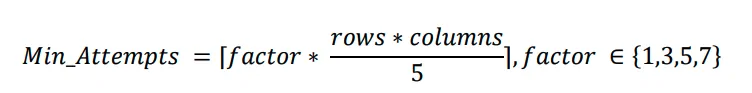
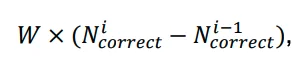
 Comprendere la demenza frontotemporale: l’importanza della psicoeducazione per i familiari
Comprendere la demenza frontotemporale: l’importanza della psicoeducazione per i familiari

Lascia un commento