Q-learning: Desde los experimentos de Pavlov a la neurorrehabilitación moderna

El Q-learning (aprendizaje Q en castellano) ha evolucionado considerablemente desde los primeros experimentos conductuales como el condicionamiento clásico de Pavlov, hasta llegar a convertirse en una de las técnicas más importantes en el ámbito del Machine Learning (aprendizaje automático). A continuación, exploraremos cómo ha sido su desarrollo y su aplicación en la neurorrehabilitación y estimulación cognitiva.

Los experimentos de Pavlov

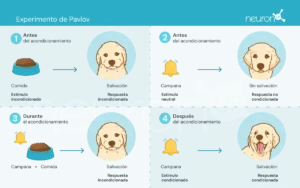
Ivan Pavlov, un fisiólogo ruso de finales del siglo XIX, es reconocido por establecer las bases de la psicología conductual a través de sus experimentos sobre el condicionamiento clásico. En estos experimentos, Pavlov demostró que los perros podían aprender a asociar un estímulo neutro, como el sonido de una campana, con un estímulo incondicionado, como la comida, provocando así una respuesta incondicionada: la salivación.

Este experimento fue fundamental para demostrar que el comportamiento puede adquirirse por asociación, un concepto crucial que posteriormente influyó en el desarrollo de las teorías de aprendizaje por refuerzo. 

Las teorías de aprendizaje por refuerzo

Estas teorías se enfocan en cómo los seres humanos y los animales aprenden conductas a partir de las consecuencias de sus acciones, lo que ha sido esencial para el diseño de algoritmos como el Q-learning.

Hay algunos conceptos clave con los que debemos familiarizarnos antes de continuar:

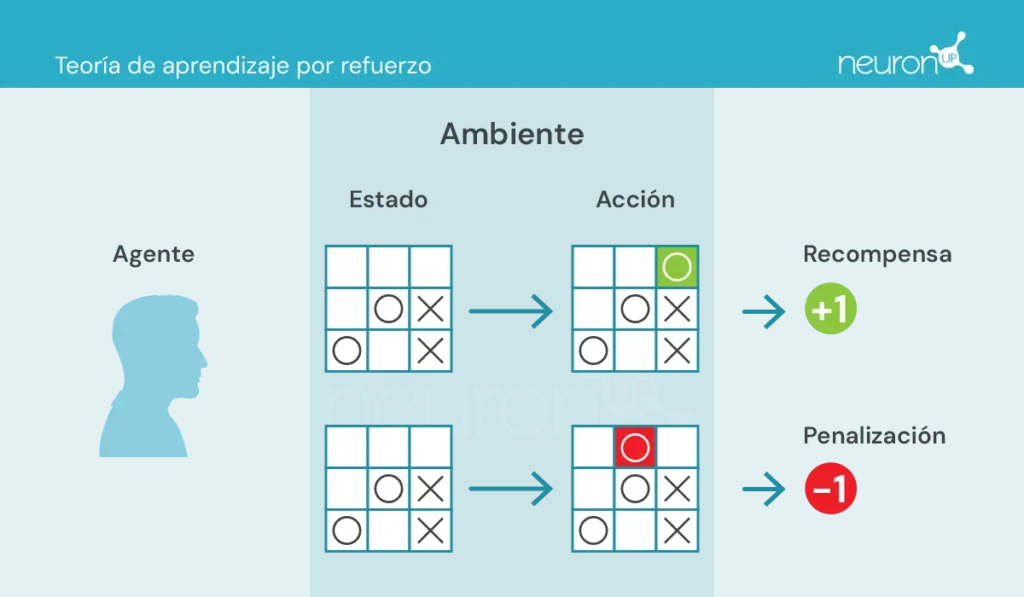
• Agente: encargado de realizar la acción.
• Ambiente: entorno donde el agente se mueve e interactúa. 
• Estado: situación actual del ambiente. 
• Acción: posibles decisiones tomadas por el agente.
• Recompensa: premios que se le otorgan al agente.

En este tipo de aprendizaje, un agente toma o realiza acciones en el entorno, recibe información en forma de recompensa/penalización y la utiliza para ajustar su comportamiento a lo largo del tiempo.

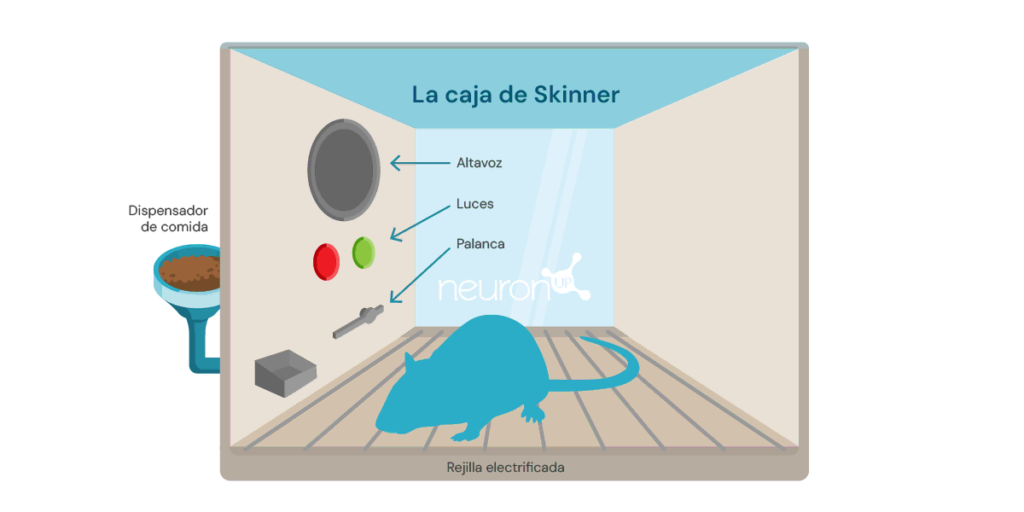
Un experimento clásico del aprendizaje por refuerzo, es el experimento de la caja de Skinner, realizado por el psicólogo estadounidense Burrhus Frederic Skinner en el año 1938. En este experimento, Skinner demostró que las ratas podían aprender a presionar una palanca para obtener comida, utilizando el refuerzo positivo como medio para modelar el comportamiento. 

El experimento consiste en introducir una rata en una caja con una palanca que pueda presionar, un dispensador de comida, y en ocasiones, una luz y un altavoz. 

Cada vez que la rata pulsa la palanca, se libera un grano de comida en el dispensador. La comida actúa como un refuerzo positivo, una recompensa por presionar la palanca. Con el tiempo, la rata empezará a presionar la palanca con más frecuencia, demostrando que ha aprendido el comportamiento a través del refuerzo.

Este tipo de aprendizaje ha servido como base para algoritmos de machine learning, como el Q-learning, que permite a las máquinas aprender comportamientos óptimos de manera autónoma mediante el método de ensayo y error.

¿Qué es el Q-learning?

El Q-learning fue introducido por Christopher Watkins en 1989 como un algoritmo de aprendizaje por refuerzo. Este algoritmo permite a un agente aprender el valor de las acciones en un estado determinado, actualizando continuamente su conocimiento a través de la experiencia, al igual que la rata de la caja de Skinner.

A diferencia de los experimentos de Pavlov, en los que el aprendizaje se basaba en asociaciones simples, el Q-learning utiliza un método más complejo de ensayo y error. El agente explora diversas acciones y actualiza una tabla Q que almacena los valores Q, los cuales representan las recompensas futuras esperadas por tomar la mejor acción en un estado específico.

El Q-learning se aplica en diversos ámbitos, como por ejemplo en sistemas de recomendación (como los utilizados por Netflix o Spotify), en vehículos autónomos (como drones o robots) y en la optimización de recursos. Ahora exploraremos cómo esta tecnología se puede aplicar en la neurorrehabilitación.

Q-learning y NeuronUP

Una de las ventajas de NeuronUP, es la capacidad de personalizar las actividades según las necesidades específicas de cada usuario. Sin embargo, personalizar cada actividad puede ser tedioso debido al elevado número de parámetros a ajustar. 

El Q-learning permite automatizar este proceso, ajustando los parámetros en función del rendimiento del usuario en las distintas actividades. Esto garantiza que los ejercicios sean exigentes pero alcanzables, mejorando la eficacia y la motivación durante la rehabilitación.

¿Cómo funciona?

En este contexto, el agente, que podría ser comparado con un usuario interactuando con una actividad, aprende a tomar decisiones óptimas en diferentes situaciones para superar correctamente la actividad. 

El Q-learning le permite al agente experimentar con diversas acciones interactuando con su entorno, recibiendo recompensas o penalizaciones, y actualizando una tabla Q que almacena estos valores Q. Estos valores representan las recompensas futuras esperadas por tomar la mejor acción en un estado específico. 

La regla de actualización de Q-learning es la siguiente:

Donde:

𝛂 – es la tasa de aprendizaje.

r – es la recompensa recibida después de tomar la acción a desde el estado s.

𝛄 – es el factor de descuento, que representa la importancia de las recompensas futuras.

s’ – es el siguiente estado.

– es el valor Q máximo para el siguiente estado s’.

Ejemplo de aplicación en una actividad de NeuronUP

Tomemos la actividad de NeuronUP llamada «Imágenes revueltas», que trabaja habilidades como la planificación, las praxias visoconstructivas y la relación espacial. En esta actividad, el objetivo es resolver un rompecabezas que ha sido mezclado y cortado en piezas. 

Las variables que definen la dificultad de esta actividad son el tamaño de la matriz (el número de filas y de columnas) así como el valor del desorden de las piezas (bajo, medio, alto o muy alto). 

Para entrenar al agente a resolver el rompecabezas, se creó una matriz de recompensas basada en el número mínimo de movimientos necesarios para resolverlo, definido por la siguiente fórmula:

La variable factor depende de la variable de desorden. Una vez creada la matriz, se aplicó un algoritmo de Q-learning para entrenar al agente a resolver el rompecabezas automáticamente. 

Esta integración incluye:

• Recuperación del valor Q: La función recupera el valor Q para un par estado-acción de la tabla Q. Si el par estado-acción no ha sido entrenado antes, devuelve 0. Esta función busca la recompensa esperada al tomar una acción específica en un estado específico.
• Actualización del valor Q: La función actualiza el valor Q para un par estado-acción basado en la recompensa recibida y el valor Q máximo del siguiente estado. Esta función implementa la regla de actualización de Q-learning mencionada anteriormente.
• Decisión sobre la acción a tomar: La función decide qué acción tomar en un estado dado, usando una estrategia epsilon-greedy. Esta estrategia equilibra la exploración y la explotación: 
  • Exploración: Consiste en seleccionar la mejor acción conocida hasta el momento. Con una probabilidad ε (tasa de exploración, un valor entre 0 y 1 que determina la probabilidad de explorar nuevas acciones en lugar de explotar las acciones conocidas), se elige una acción aleatoria, permitiendo al agente descubrir acciones potencialmente mejores. 
  •  Explotación: Consiste en probar acciones diferentes a las mejores conocidas para descubrir si pueden ofrecer mejores recompensas en el futuro. Con una probabilidad 1−ε, el agente selecciona la acción con el valor Q más alto para el estado actual, utilizando su conocimiento aprendido: a’ = argmaxaQ(s,a). Donde a’ es la acción que maximiza la función Q en un estado s dado. Esto significa que, dado un estado s, seleccione la acción a que tiene el valor Q más alto.

Estas funciones trabajan juntas para permitir que el algoritmo de Q-learning desarrolle una estrategia óptima para resolver el rompecabezas.

Análisis preliminar de la ejecución del algoritmo

Se aplicó el algoritmo a un rompecabezas de matriz 2×3 con un factor de dificultad de  1 (bajo), correspondiente a un número mínimo de intentos igual a 2. El algoritmo se ejecutó en el mismo rompecabezas 20 veces, aplicando la misma configuración de mezclado en cada ocasión y actualizando la tabla Q después de cada paso. Después de 20 ejecuciones, el rompecabezas se mezcló en una configuración diferente y el proceso se repitió, resultando en un total de 2000 iteraciones. Los valores iniciales de los parámetros fueron: 

• Recompensa por resolver el rompecabezas: 100 puntos 
• Penalización por cada movimiento: -1 punto

En cada paso, se aplicaba una recompensa o penalización adicional basada en el número de piezas correcta, permitiendo al agente comprender su progreso hacia la solución del rompecabezas. Esto se calculaba utilizando la fórmula:

Donde:

• W es el factor de peso.
• es el número de piezas correctas después del movimiento.
• es el número de piezas correctas antes del movimiento.

El gráfico a continuación ilustra el número de movimientos necesarios por iteración para que el modelo resuelva un rompecabezas de tamaño 2×3. Al inicio, el modelo requiere un gran número de movimientos, lo que refleja su falta de conocimiento sobre cómo resolver el rompecabezas de manera eficiente. Sin embargo, a medida que el algoritmo de Q-learning se entrena, se observa una tendencia a la baja en el número de movimientos, lo que sugiere que el modelo está aprendiendo a optimizar su proceso de resolución.

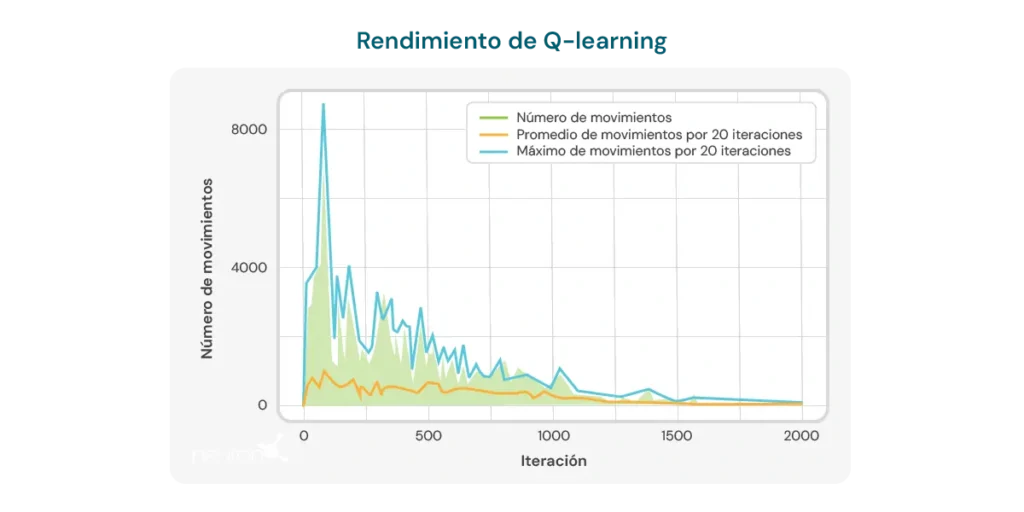
Esta tendencia es un indicio positivo del potencial del algoritmo para mejorar con el tiempo. Sin embargo, se deben considerar varias limitaciones importantes:

• Tamaño específico del puzzle: El algoritmo demuestra eficacia principalmente en puzzles con un tamaño específico, como el de matriz 2×3. Al cambiar el tamaño o la complejidad del puzzle, el rendimiento del algoritmo puede disminuir significativamente.
• Tiempo de cálculo: Cuando se aplica el algoritmo a configuraciones diferentes o más complejas, el tiempo necesario para realizar los cálculos y resolver el puzzle aumenta considerablemente. Esto limita su aplicabilidad en situaciones que requieren respuestas rápidas o en puzzles con una mayor complejidad.
• Número de movimientos aún alto: A pesar de la mejora observada, el número de movimientos requeridos para resolver el puzzle sigue siendo relativamente alto, incluso después de múltiples iteraciones. En las últimas ejecuciones, el modelo requiere un promedio de 8 a 10 movimientos, lo que indica que todavía hay margen para mejorar la eficiencia del aprendizaje.

Estas limitaciones subrayan la necesidad de un refinamiento adicional del algoritmo, ya sea ajustando los parámetros de aprendizaje, mejorando la estructura del modelo o incorporando técnicas complementarias que permitan un aprendizaje más eficiente y adaptable a diferentes configuraciones de puzzles. A pesar de estas limitaciones, no debemos olvidarnos de las ventajas que ofrece el Q-learning en la neurorrehabilitación, entre ellas:

• La personalización dinámica de las actividades: El Q-learning es capaz de ajustar automáticamente los parámetros de las actividades terapéuticas en función del rendimiento individual del usuario. Esto significa que las actividades se pueden personalizar en tiempo real, asegurando que cada usuario trabaje a un nivel que sea desafiante pero alcanzable. Esto es especialmente útil en neurorrehabilitación, donde las capacidades de los usuarios pueden variar considerablemente y cambiar a lo largo del tiempo.
• Un incremento de la motivación y del compromiso: A medida que las actividades se adaptan constantemente al nivel de habilidad del usuario, se evita la frustración por tareas demasiado difíciles o el aburrimiento por tareas demasiado simples. Esto puede aumentar significativamente la motivación del usuario y su compromiso con el programa de rehabilitación, lo que es crucial para lograr resultados exitosos.
• La optimización del proceso de aprendizaje: Al utilizar Q-learning, el sistema puede aprender de las interacciones anteriores del usuario con las actividades, optimizando el proceso de aprendizaje y rehabilitación. Esto permite que los ejercicios sean más efectivos, centrándose en áreas donde el usuario necesita más atención y reduciendo el tiempo necesario para alcanzar los objetivos terapéuticos.
• Eficiencia en la toma de decisiones clínicas: Los profesionales pueden beneficiarse del Q-learning al obtener recomendaciones basadas en datos sobre cómo ajustar las terapias. Esto facilita la toma de decisiones clínicas más informadas y precisas, lo que a su vez mejora la calidad de la atención proporcionada al usuario.
• Mejora continua: A lo largo del tiempo, el sistema basado en Q-learning puede mejorar su rendimiento mediante la acumulación de datos y la experiencia del usuario. Esto significa que, cuanto más se use el sistema, más eficaz se vuelve en la personalización y optimización de los ejercicios, ofreciendo así una ventaja a largo plazo en el proceso de neurorrehabilitación.

Concluyendo, el Q-learning ha evolucionado desde sus raíces en la psicología conductual hasta convertirse en una herramienta poderosa en la inteligencia artificial y la neurorrehabilitación. Su capacidad para adaptar actividades de manera autónoma lo convierte en un recurso valioso para mejorar la eficacia de las terapias de rehabilitación, aunque aún existen desafíos que superar para optimizar completamente su aplicación.

Bibliografía

• Bermejo Fernández, E. (2017). Aplicación de algoritmos de reinforcement learning a juegos.
• Giró Gràcia, X., & Sancho Gil, J. M. (2022). La Inteligencia Artificial en la educación: Big data, cajas negras y solucionismo tecnológico.
• Meyn, S. (2023). Stability of Q-learning through design and optimism. arXiv preprint arXiv:2307.02632.
• Morinigo, C., & Fenner, I. (2021). Teorías del aprendizaje. Minerva Magazine of Science, 9(2), 1-36.
• M.-V. Aponte, G. Levieux y S. Natkin. (2009). Measuring the level of difficulty in single player video games. Entertainment Computing.
• P. Jan L., H. Bruce D., P. Shashank, B. Corinne J., & M. Andrew P. (2019). The Effect of Adaptive Difficulty Adjustment on the Effectiveness of a Game to Develop Executive Function Skills for Learners of Different Ages. Cognitive Development, pp. 49, 56–67.
• R. Anna N., Z. Matei & G. Thomas L. Optimally Designing Games for Cognitive Science Research. Computer Science Division and Department of Psychology, University of California, Berkeley.
• Toledo Sánchez, M. (2024). Aplicaciones del aprendizaje por refuerzo en videojuegos.

Si te ha gustado este artículo acerca del Q-learning, seguramente te interesen estos artículos de NeuronUP: