Q-learning: من تجارب بافلوف إلى إعادة التأهيل العصبي الحديث

تطور Q-learning (التعلّم Q بالعربية) بشكل كبير منذ التجارب السلوكية الأولى مثل التعويد الكلاسيكي عند بافلوف، حتى أصبح واحدًا من أهم التقنيات في مجال تعلم الآلة (Machine Learning). فيما يلي سنستعرض كيف كان تطوره وتطبيقه في التأهيل العصبي والتحفيز المعرفي.

تجارب بافلوف

إيفان بافلوف، عالم فسيولوجيا روسي من أواخر القرن التاسع عشر، معروف بوضع أسس علم النفس السلوكي من خلال تجاربه على التعويد الكلاسيكي. في هذه التجارب، أظهر بافلوف أن الكلاب يمكنها أن تتعلّم ربط منشط محايد، مثل صوت جرس، بمنشط غير مشروط، مثل الطعام، مما يستدعي استجابة غير مشروطة: الإفراز اللعابي.

كانت هذه التجربة أساسية لإظهار أن السلوك يمكن اكتسابه بالارتباط، وهو مفهوم حاسم أثر لاحقًا في تطوير نظريات التعلم المعزز. 

نظريات التعلم المعزز

تركز هذه النظريات على كيف يتعلم البشر والحيوانات السلوكيات من عواقب أفعالهم، وهو ما كان أساسيًا في تصميم خوارزميات مثل Q-learning.

هناك بعض المفاهيم الأساسية التي يجب أن نألفها قبل المتابعة:

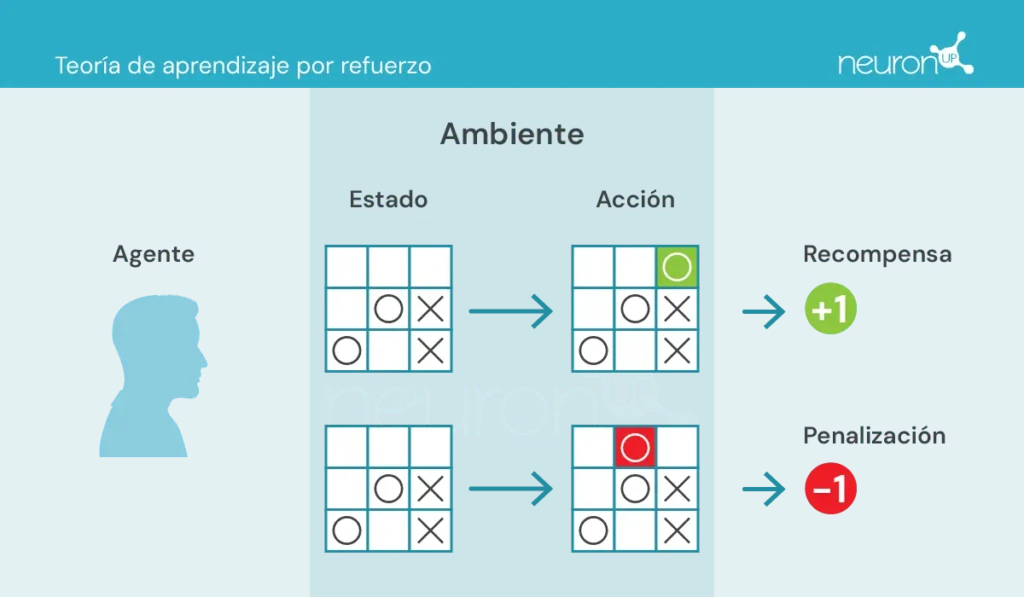
• الوكيل (Agente): المسؤول عن تنفيذ الفعل.
• البيئة (Ambiente): الوسط الذي يتحرك فيه الوكيل ويتفاعل معه. 
• الحالة (Estado): الوضع الحالي للبيئة. 
• الفعل (Acción): القرارات الممكنة التي يتخذها الوكيل.
• المكافأة (Recompensa): المكافآت التي تُمنح للوكيل.

في هذا النوع من التعلم، يتخذ الوكيل إجراءات في البيئة، ويتلقى معلومات على شكل مكافأة/عقاب ويستخدمها لتعديل سلوكه بمرور الوقت.

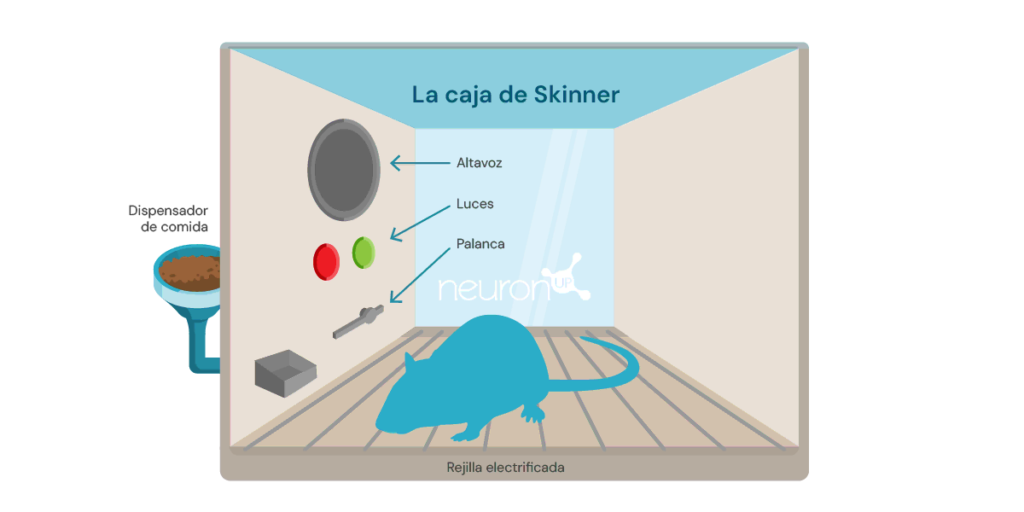
تجربة كلاسيكية في التعلم المعزز هي تجربة صندوق سكينر، التي أجراها عالم النفس الأمريكي بورهس فريدريك سكينر عام 1938. في هذه التجربة، أظهر سكينر أن الفئران يمكنها أن تتعلم الضغط على رافعة للحصول على الطعام، باستخدام التعزيز الإيجابي كوسيلة لتشكيل السلوك. 

تتألف التجربة من وضع فأر في صندوق يحتوي على رافعة يمكنه الضغط عليها، وموزع طعام، وفي بعض الأحيان ضوء ومكبر صوت. 

في كل مرة يضغط فيها الفأر على الرافعة، يُفلت حبة طعام في الموزع. يعمل الطعام كمكافأة إيجابية، مكافأة على الضغط على الرافعة. مع مرور الوقت، سيبدأ الفأر بالضغط على الرافعة بتكرار أكبر، مما يدل على أنه تعلم السلوك من خلال التعزيز.

خدم هذا النوع من التعلم كأساس لخوارزميات تعلم الآلة مثل Q-learning، الذي يسمح للآلات بتعلم سلوكيات مثلى بشكل ذاتي من خلال طريقة التجربة والخطأ.

ما هو Q-learning؟

قدم Q-learning كريستوفر واتكينز في عام 1989 كخوارزمية للتعلم المعزز. تتيح هذه الخوارزمية لوكيل أن يتعلم قيمة الأفعال في حالة معينة، محدثًا معرفته باستمرار من خلال الخبرة، تمامًا كما في تجربة الفأر في صندوق سكينر.

على عكس تجارب بافلوف التي كان التعلم فيها قائمًا على ارتباطات بسيطة، يستخدم Q-learning طريقة أكثر تعقيدًا من التجربة والخطأ. يستكشف الوكيل أفعالًا مختلفة ويحدّث جدول Q الذي يخزن قيم Q، والتي تمثل المكافآت المستقبلية المتوقعة لاتخاذ أفضل فعل في حالة محددة.

يُطبق Q-learning في مجالات متنوعة، مثل نظم التوصية (كالتي تستخدمها Netflix أو Spotify)، في المركبات الذاتية (كالطائرات بدون طيار أو الروبوتات) وفي تحسين الموارد. الآن سنستعرض كيف يمكن تطبيق هذه التقنية في التأهيل العصبي.

Q-learning و NeuronUP

من مزايا NeuronUP القدرة على تخصيص الأنشطة وفق الاحتياجات الخاصة بكل مستخدم. ومع ذلك، قد يكون تخصيص كل نشاط مرهقًا بسبب العدد الكبير من المعاملات التي يجب ضبطها. 

يتيح Q-learning أتمتة هذه العملية، بتعديل المعاملات بناءً على أداء المستخدم في الأنشطة المختلفة. هذا يضمن أن تكون التمارين متطلبة لكن قابلة للتحقيق، محسنًا الفعالية والتحفيز أثناء التأهيل.

كيف تعمل؟

في هذا السياق، الوكيل، الذي يمكن مقارنته بمستخدم يتفاعل مع نشاط، يتعلّم اتخاذ قرارات مثلى في مواقف مختلفة للتغلب على النشاط بنجاح. 

يتيح Q-learning للوكيل تجربة أفعال متنوعة بالتفاعل مع بيئته، وتلقي مكافآت أو عقوبات، وتحديث جدول Q الذي يخزن هذه قيم Q. تمثل هذه القيم المكافآت المستقبلية المتوقعة عند اتخاذ أفضل فعل في حالة معينة. 

قاعدة تحديث Q-learning هي كما يلي:

\[Q(s,a) \leftarrow Q(s,a) + \alpha\bigl(r + \gamma \cdot \max_{a’}\bigl(Q(s’,a’)\bigr) – Q(s,a)\bigr)\]

حيث:

𝛂 – هو معدل التعلّم.

r – هي المكافأة المستلمة بعد اتخاذ الفعل a من الحالة s.

𝛄 – هو عامل الخصم، الذي يمثل أهمية المكافآت المستقبلية.

s’ – هي الحالة التالية.

\(\max_{a’}\bigl(Q(s’,a’)\bigr)\) – هي قيمة Q العظمى للحالة التالية s’.

مثال لتطبيق في نشاط من NeuronUP

لنأخذ نشاط NeuronUP المسمى “Imágenes revueltas” الذي يعمل على مهارات مثل التخطيط، المهارات البراكسية البنائية البصرية والعلاقة المكانية. في هذا النشاط، الهدف هو حل لغز تم خلطه وتقطيعه إلى قطع. 

المتغيرات التي تحدد صعوبة هذا النشاط هي حجم المصفوفة (عدد الصفوف والأعمدة) بالإضافة إلى قيمة عشوائية خلط القطع (منخفض، متوسط، عالي أو عالي جدًا). 

لتدريب الوكيل على حل اللغز، تم إنشاء مصفوفة مكافآت بناءً على الحد الأدنى لعدد الحركات اللازمة لحله، والمعرّفة بالصيغة التالية:

\[\mathrm{Min\_Attempts} \;=\;\left\lceil \frac{\mathrm{factor} * \mathrm{rows} * \mathrm{columns}}{5}\right\rceil,\quad \mathrm{factor}\in\{1,3,5,7\}\]

تعتمد متغيرات factor على متغير العشوائية. بعد إنشاء المصفوفة، طُبّق خوارزم Q-learning لتدريب الوكيل على حل اللغز تلقائيًا. 

يتضمن هذا التكامل:

• استرجاع قيمة Q: تقوم الدالة باسترجاع قيمة Q لزوج حالة-فعل من جدول Q. إذا لم يتم تدريب زوج الحالة-الفعل من قبل، تُعيد 0. تبحث هذه الدالة عن المكافأة المتوقعة عند اتخاذ فعل معيّن في حالة معيّنة.
• تحديث قيمة Q: تقوم الدالة بتحديث قيمة Q لزوج حالة-فعل بناءً على المكافأة المستلمة وقيمة Q العظمى للحالة التالية. تنفّذ هذه الدالة قاعدة تحديث Q-learning المذكورة أعلاه.
• اتخاذ القرار بشأن الفعل الذي يجب اتخاذه: تقرر الدالة أي فعل تُتخذ في حالة معيّنة، مستخدمة استراتيجية epsilon-greedy. توازن هذه الاستراتيجية بين الاستكشاف والاستغلال: 
  • الاستكشاف: يتكون من اختيار أفضل فعل معروف حتى الآن. باحتمالية ε (معدل الاستكشاف، قيمة بين 0 و1 تحدد احتمال استكشاف أفعال جديدة بدلاً من استغلال الأفعال المعروفة)، يُختار فعل عشوائي، مما يتيح للوكيل اكتشاف أفعال قد تكون أفضل. 
  •  الاستغلال: يتكون من تجربة أفعال مختلفة عن الأفضل المعروف لاكتشاف ما إذا كانت قد تقدم مكافآت أفضل في المستقبل. باحتمالية 1−ε، يختار الوكيل الفعل الذي له أعلى قيمة Q للحالة الحالية، مستخدمًا معرفته المتعلّمة: a’ = argmaxaQ(s,a). حيث a’ هو الفعل الذي يُعظّم الدالة Q في الحالة s المعطاة. هذا يعني أنه، بالنظر إلى حالة s، اختَر الفعل a الذي له أعلى قيمة Q.

تعمل هذه الدوال معًا لتمكين خوارزمية Q-learning من تطوير استراتيجية مثلى لحل اللغز.

تحليل أولي لتنفيذ الخوارزم

طُبّق الخوارزم على لغز بمصفوفة 2×3 مع عامل صعوبة قيمته  1 (منخفض)، مما يعادل عددًا أدنى من المحاولات يساوي 2. شُغّل الخوارزم على نفس اللغز 20 مرة، مع تطبيق نفس إعداد الخلط في كل مرة وتحديث جدول Q بعد كل خطوة. بعد 20 تنفيذًا، خُلط اللغز في إعداد مختلف وتكرر العملية، مما أدى إلى ما مجموعه 2000 تكرار. كانت القيم الأولية للمعاملات: 

• مكافأة لحل اللغز: 100 نقطة 
• عقوبة عن كل حركة: -1 نقطة

في كل خطوة، كانت تُطبّق مكافأة أو عقوبة إضافية بناءً على عدد القطع الصحيحة، مما يتيح للوكيل فهم تقدمه نحو حل اللغز. هذا كان يُحسب باستخدام الصيغة:

\[W \times \bigl(N_{\mathrm{correct}}^i \;-\; N_{\mathrm{correct}}^{\,i-1}\bigr)\]

حيث:

• W هو عامل الوزن.
• \(N_{\mathrm{correct}}^{\,i}\) هو عدد القطع الصحيحة بعد الحركة.
• \(N_{\mathrm{correct}}^{\,i-1}\) هو عدد القطع الصحيحة قبل الحركة.

الرسم البياني أدناه يوضّح عدد الحركات اللازمة لكل تكرار حتى يحل النموذج لغزًا بحجم 2×3. في البداية، يتطلب النموذج عددًا كبيرًا من الحركات، مما يعكس افتقاره إلى المعرفة حول كيفية حل اللغز بكفاءة. ومع ذلك، مع تدريب خوارزم Q-learning، يُلاحظ اتجاه هبوطي في عدد الحركات، ما يوحي بأن النموذج يتعلّم تحسين عملية الحل.

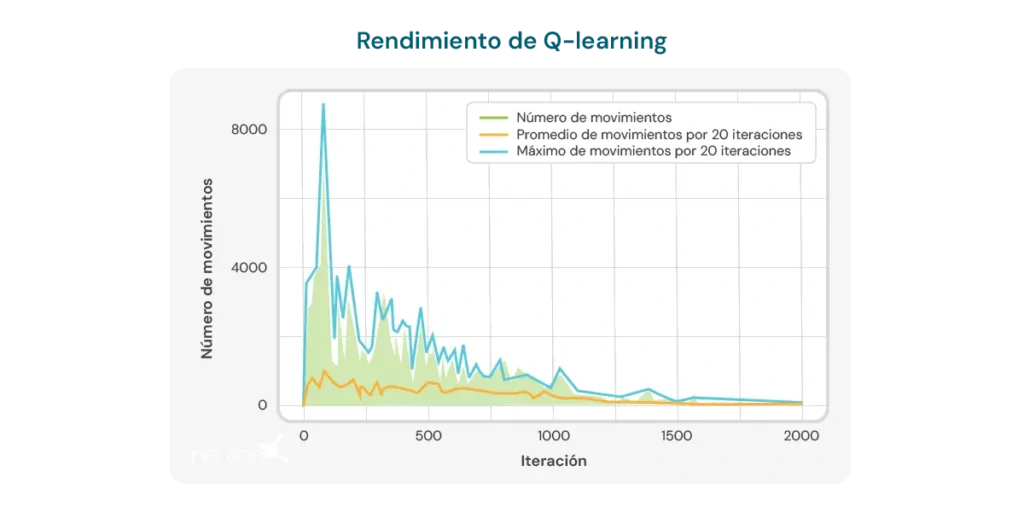
هذا الاتجاه مؤشر إيجابي على قدرة الخوارزم على التحسّن مع الوقت. ومع ذلك، يجب مراعاة عدة محدوديات هامة:

• حجم اللغز محدد: تُظهر الخوارزمية فعالية في الغالب على الألغاز ذات حجم محدد، مثل مصفوفة 2×3. عند تغيير الحجم أو تعقيد اللغز، قد ينخفض أداء الخوارزمية بشكل كبير.
• زمن الحساب: عند تطبيق الخوارزمية على إعدادات مختلفة أو أكثر تعقيدًا، يزداد الوقت اللازم لإجراء الحسابات وحل اللغز بشكل كبير. هذا يحد من قابليتها للتطبيق في مواقف تتطلب استجابات سريعة أو في ألغاز ذات تعقيد أعلى.
• عدد الحركات لا يزال مرتفعًا: رغم التحسن الملحوظ، فإن عدد الحركات المطلوبة لحل اللغز يبقى مرتفعًا نسبيًا، حتى بعد عدة تكرارات. في التنفيذات الأخيرة، يحتاج النموذج في المتوسط من 8 إلى 10 حركات، مما يشير إلى وجود مجال لتحسين كفاءة التعلم.

تؤكد هذه المحدوديات الحاجة إلى مزيد من تحسين الخوارزم، سواء عبر ضبط معاملات التعلم، تحسين بنية النموذج أو دمج تقنيات مكملة تسمح بتعلّم أكثر كفاءة وقابلية للتكيف مع إعدادات ألغاز مختلفة. على الرغم من هذه المحدوديات، لا ينبغي أن نغفل عن المزايا التي يقدمها Q-learning في التأهيل العصبي، ومنها:

• التخصيص الديناميكي للأنشطة: يستطيع Q-learning ضبط معاملات الأنشطة العلاجية تلقائيًا بناءً على أداء المستخدم الفردي. هذا يعني أنه يمكن تخصيص الأنشطة في الوقت الفعلي، مما يضمن أن يعمل كل مستخدم على مستوى يكون فيه التحدي مناسبًا لكنه قابل للتحقيق. هذا مفيد بشكل خاص في التأهيل العصبي حيث قد تختلف قدرات المستخدمين اختلافًا كبيرًا وتتغير مع مرور الوقت.
• زيادة التحفيز والالتزام: مع تكيف الأنشطة باستمرار مع مستوى مهارة المستخدم، يتم تجنب الإحباط الناتج عن مهام صعبة جدًا أو الملل الناتج عن مهام بسيطة جدًا. هذا يمكن أن يزيد بشكل ملحوظ من تحفيز المستخدم والتزامه ببرنامج التأهيل، وهو أمر حاسم لتحقيق نتائج ناجحة.
• تحسين عملية التعلم: باستخدام Q-learning، يمكن للنظام أن يتعلم من تفاعلات المستخدم السابقة مع الأنشطة، محسنًا عملية التعلم والتأهيل. هذا يسمح بأن تكون التمارين أكثر فعالية، مركزة على المناطق التي يحتاج فيها المستخدم إلى مزيد من الانتباه، ومقللة الوقت اللازم لتحقيق الأهداف العلاجية.
• الكفاءة في اتخاذ القرارات السريرية: يمكن للمهنيين الاستفادة من Q-learning بالحصول على توصيات قائمة على البيانات حول كيفية تعديل العلاجات. هذا يسهل اتخاذ قرارات سريرية أكثر استنارة ودقة، مما يحسّن جودة الرعاية المقدمة للمستخدم.
• التحسن المستمر: مع مرور الوقت، يمكن للنظام المعتمد على Q-learning تحسين أدائه من خلال تراكم البيانات وخبرة المستخدم. هذا يعني أنه كلما استُخدم النظام أكثر، أصبح أكثر فعالية في التخصيص والتحسين، مقدمًا ميزة طويلة الأمد في عملية التأهيل العصبي.

خلاصة القول، تطور Q-learning من جذوره في علم النفس السلوكي إلى أن أصبح أداة قوية في الذكاء الاصطناعي والتأهيل العصبي. قدرته على تكييف الأنشطة بشكل ذاتي تجعله مورداً قيمًا لتحسين فعالية علاجات التأهيل، على الرغم من وجود تحديات لا تزال تحتاج إلى تجاوز لتحقيق تطبيق أمثل بالكامل.

المراجع

• Bermejo Fernández, E. (2017). تطبيق خوارزميات التعلم المعزز على الألعاب.
• Giró Gràcia, X., & Sancho Gil, J. M. (2022). الذكاء الاصطناعي في التعليم: البيانات الضخمة، الصناديق السوداء والحلّ التقني.
• Meyn, S. (2023). Stability of Q-learning through design and optimism. arXiv preprint arXiv:2307.02632.
• Morinigo, C., & Fenner, I. (2021). نظريات التعلم. Minerva Magazine of Science, 9(2), 1-36.
• M.-V. Aponte, G. Levieux y S. Natkin. (2009). Measuring the level of difficulty in single player video games. Entertainment Computing.
• P. Jan L., H. Bruce D., P. Shashank, B. Corinne J., & M. Andrew P. (2019). The Effect of Adaptive Difficulty Adjustment on the Effectiveness of a Game to Develop Executive Function Skills for Learners of Different Ages. Cognitive Development, pp. 49, 56–67.
• R. Anna N., Z. Matei & G. Thomas L. Optimally Designing Games for Cognitive Science Research. Computer Science Division and Department of Psychology, University of California, Berkeley.
• Toledo Sánchez, M. (2024). تطبيقات التعلم المعزز في ألعاب الفيديو.

إذا أعجبك هذا المقال عن Q-learning، فربما تهمك هذه المقالات من NeuronUP:

“تمت ترجمة هذا المقال. رابط المقال الأصلي باللغة الإسبانية:”
Q-learning: Desde los experimentos de Pavlov a la neurorrehabilitación moderna